I’m thrilled to announce Swift Collections, a new open-source package focused on extending the set of available Swift data structures. Like the Swift Algorithms and Swift Numerics packages before it, we’re releasing Swift Collections to help incubate new functionality for the Swift Standard Library.

The Swift Standard Library currently implements the three most essential general-purpose data structures: Array, Set and Dictionary. These are the right tool for a wide variety of use cases, and they are particularly well-suited for use as currency types. But sometimes, in order to efficiently solve a problem or to maintain an invariant, Swift programmers would benefit from a larger library of data structures.

We expect the Collections package to empower you to write faster and more reliable programs, with less effort.

A Brief Tour

The initial version of the Collections package contains implementations for three of the most frequently requested data structures: a double-ended queue (or “deque”, for short), an ordered set and an ordered dictionary.

Deque

Deque (pronounced “deck”) works much like Array: it is an ordered, random-access, mutable, range-replaceable collection with integer indices.

The main benefit of Deque over Array is that it supports efficient insertions and removals at both ends.

This makes deques a great choice whenever we need a first-in-first-out queue. To emphasize this, Deque provides convenient operations to insert and pop elements at both ends:

<span class="k">var</span> <span class="nv">colors</span><span class="p">:</span> <span class="kt">Deque</span> <span class="o">=</span> <span class="p">[</span><span class="s">"red"</span><span class="p">,</span> <span class="s">"yellow"</span><span class="p">,</span> <span class="s">"blue"</span><span class="p">]</span>

<span class="n">colors</span><span class="o">.</span><span class="nf">prepend</span><span class="p">(</span><span class="s">"green"</span><span class="p">)</span>
<span class="n">colors</span><span class="o">.</span><span class="nf">append</span><span class="p">(</span><span class="s">"orange"</span><span class="p">)</span>
<span class="c1">// `colors` is now ["green", "red", "yellow", "blue", "orange"]</span>

<span class="n">colors</span><span class="o">.</span><span class="nf">popFirst</span><span class="p">()</span> <span class="c1">// "green"</span>
<span class="n">colors</span><span class="o">.</span><span class="nf">popLast</span><span class="p">()</span> <span class="c1">// "orange"</span>
<span class="c1">// `colors` is back to ["red", "yellow", "blue"]</span>

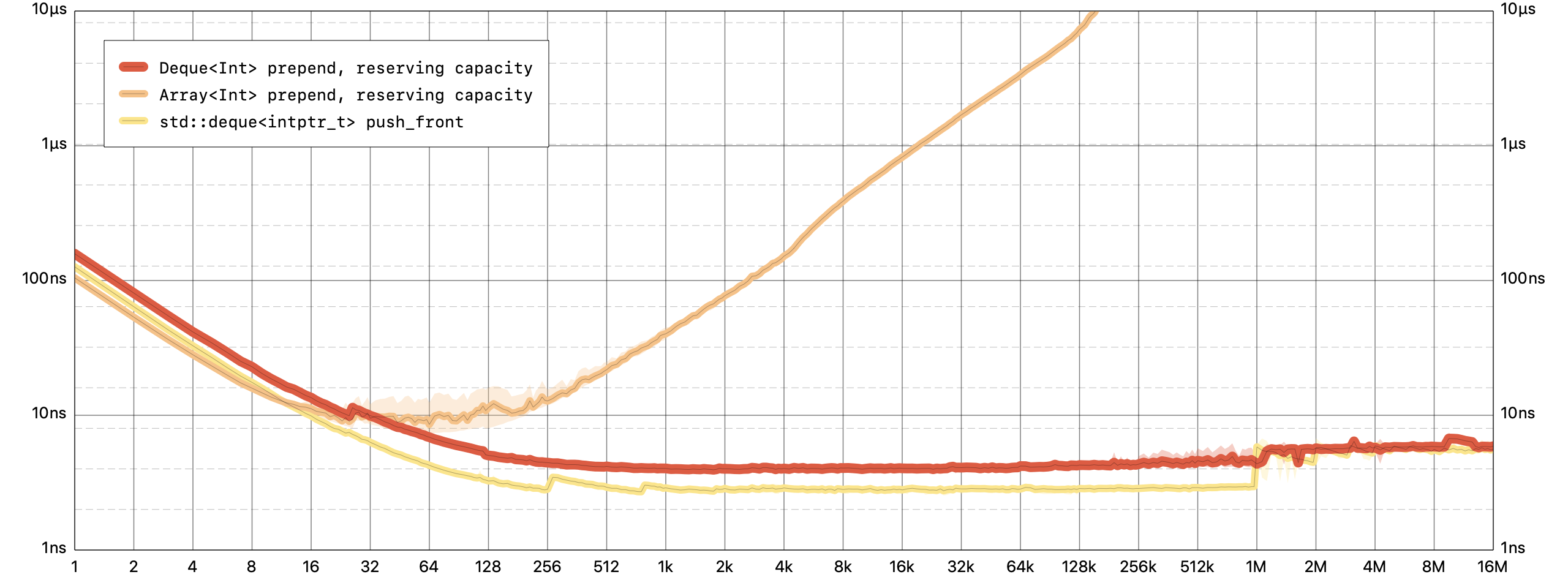
Prepending an element is a constant time operation for Deque, but a linear time operation for Array.

Note: All graphs plot the average per-element processing time on a log-log scale. Lower is better. The benchmarks were run on my 2017 iMac Pro.

Of course, we can also use any of the familiar MutableCollection and RangeReplaceableCollection methods to access and mutate elements of the collection. Indices work exactly like the do in an Array – the first element is always at index zero:

<span class="n">colors</span><span class="p">[</span><span class="mi">1</span><span class="p">]</span> <span class="c1">// "yellow"</span>
<span class="n">colors</span><span class="p">[</span><span class="mi">1</span><span class="p">]</span> <span class="o">=</span> <span class="s">"peach"</span>
<span class="n">colors</span><span class="o">.</span><span class="nf">insert</span><span class="p">(</span><span class="nv">contentsOf</span><span class="p">:</span> <span class="p">[</span><span class="s">"violet"</span><span class="p">,</span> <span class="s">"pink"</span><span class="p">],</span> <span class="nv">at</span><span class="p">:</span> <span class="mi">1</span><span class="p">)</span>
<span class="c1">// `colors` is now ["red", "violet", "pink", "peach", "blue"]</span>
<span class="n">colors</span><span class="o">.</span><span class="nf">remove</span><span class="p">(</span><span class="nv">at</span><span class="p">:</span> <span class="mi">2</span><span class="p">)</span> <span class="c1">// "pink"</span>
<span class="c1">// `colors` is now ["red", "violet", "peach", "blue"]</span>
<span class="n">colors</span><span class="o">.</span><span class="nf">sort</span><span class="p">()</span>
<span class="c1">// `colors` is now ["blue", "peach", "red", "violet"]</span>

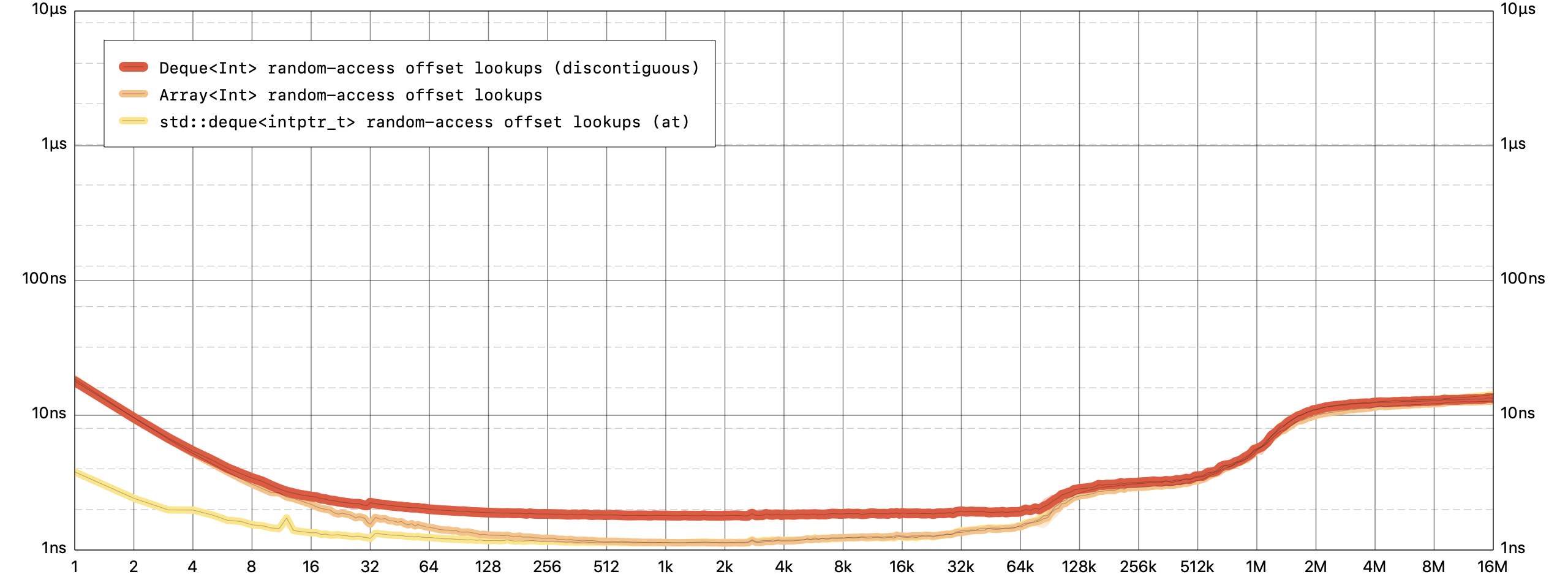
Like Array, accessing an element at an arbirary offset is a constant time operation for Deque.

To support efficient insertions at the front, deques need to give up on maintaining their elements in a contiguous buffer. This tends to make them work slightly slower than arrays for use cases that don’t call for inserting/removing elements at the front – so it’s probably not a good idea to blindly replace all your arrays with deques.

OrderedSet

OrderedSet is a powerful hybrid of an Array and a Set.

We can create an ordered set with any element type that conforms to the Hashable protocol:

<span class="k">let</span> <span class="nv">buildingMaterials</span><span class="p">:</span> <span class="kt">OrderedSet</span> <span class="o">=</span> <span class="p">[</span><span class="s">"straw"</span><span class="p">,</span> <span class="s">"sticks"</span><span class="p">,</span> <span class="s">"bricks"</span><span class="p">]</span>

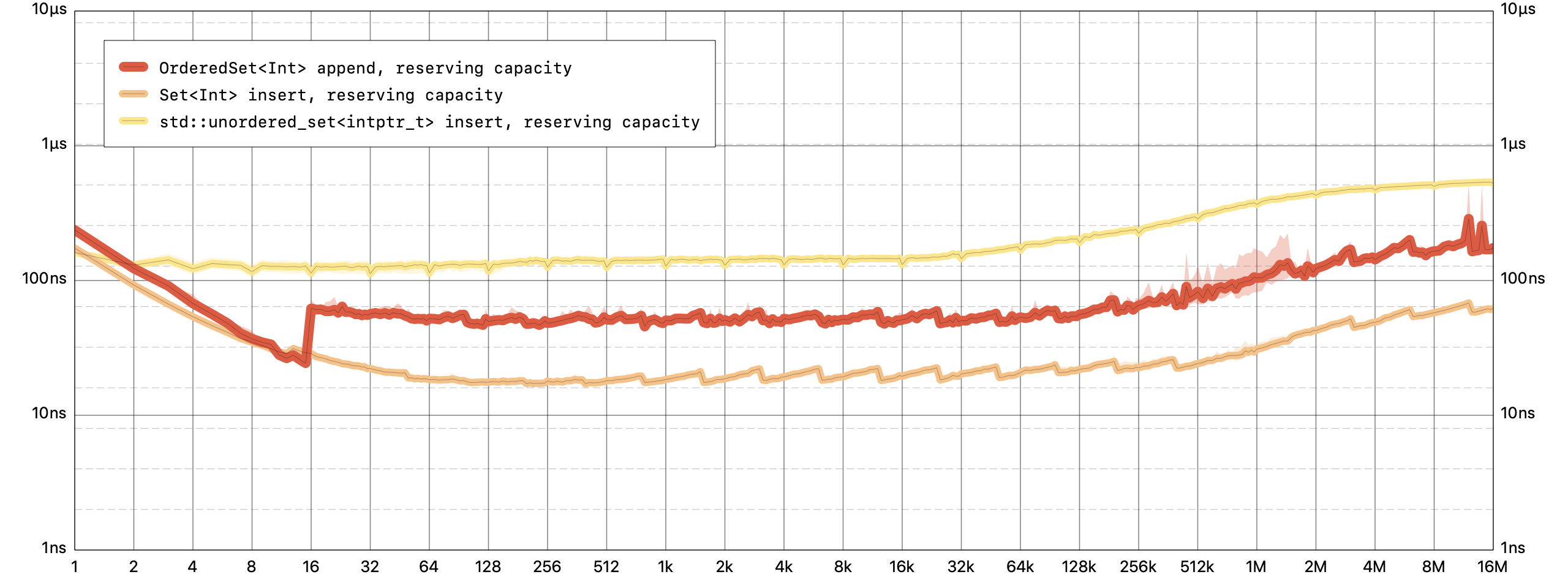
Appending an element, which includes ensuring it’s unique, is a constant time operation for OrderedSet.

Note: All benchmarks configured std::unordered_set and std::unordered_map to use the same hash function as Swift, in order to compare like to like.

Like Array, ordered sets maintain their elements in a user-specified order and support efficient random-access traversal of their members:

<span class="k">for</span> <span class="n">i</span> <span class="k">in</span> <span class="mi">0</span> <span class="o">..<</span> <span class="n">buildingMaterials</span><span class="o">.</span><span class="n">count</span> <span class="p">{</span>
  <span class="nf">print</span><span class="p">(</span><span class="s">"Little piggie #</span><span class="se">\(</span><span class="n">i</span><span class="se">)</span><span class="s"> built a house of </span><span class="se">\(</span><span class="n">buildingMaterials</span><span class="p">[</span><span class="n">i</span><span class="p">]</span><span class="se">)</span><span class="s">"</span><span class="p">)</span>
<span class="p">}</span>
<span class="c1">// Little piggie #0 built a house of straw</span>
<span class="c1">// Little piggie #1 built a house of sticks</span>
<span class="c1">// Little piggie #2 built a house of bricks</span>

Like a Set, ordered sets ensure each element appears only once and provides efficient tests for membership:

<span class="n">buildingMaterials</span><span class="o">.</span><span class="nf">append</span><span class="p">(</span><span class="s">"straw"</span><span class="p">)</span> <span class="c1">// (inserted: false, index: 0)</span>
<span class="n">buildingMaterials</span><span class="o">.</span><span class="nf">contains</span><span class="p">(</span><span class="s">"glass"</span><span class="p">)</span> <span class="c1">// false</span>
<span class="n">buildingMaterials</span><span class="o">.</span><span class="nf">append</span><span class="p">(</span><span class="s">"glass"</span><span class="p">)</span> <span class="c1">// (inserted: true, index: 3)</span>
<span class="c1">// `buildingMaterials` is now ["straw", "sticks", "bricks", "glass"]</span>

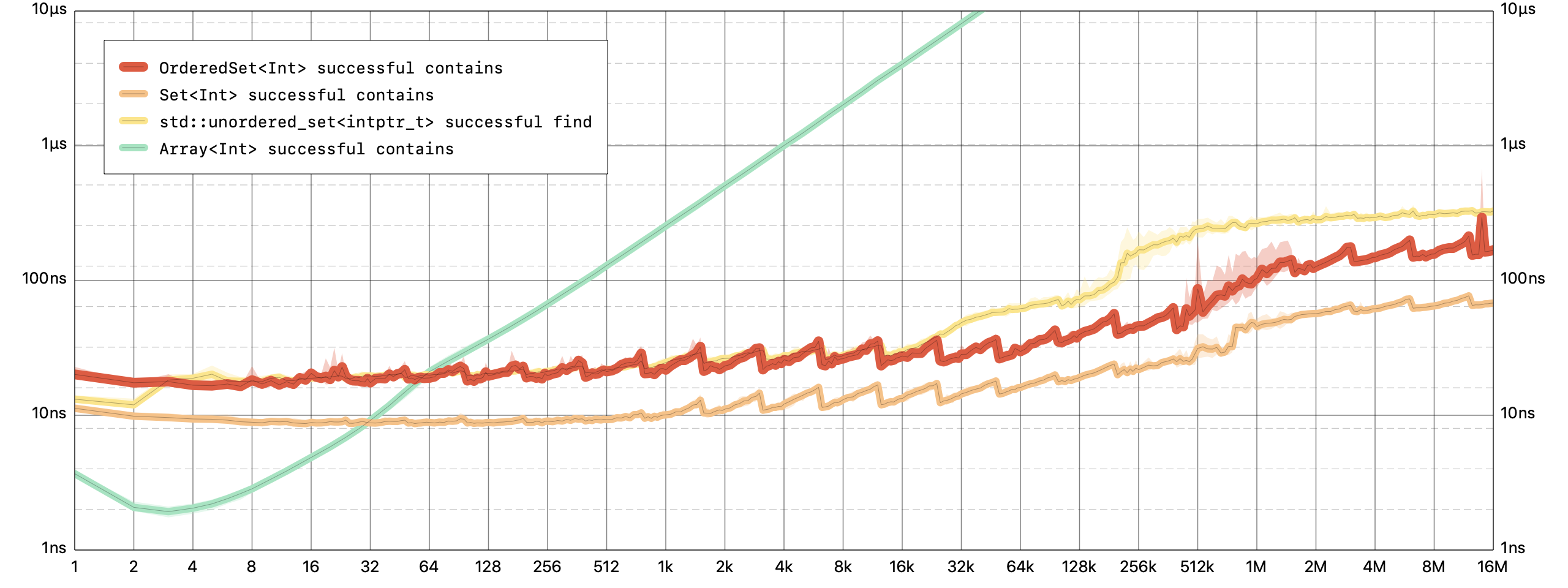
Membership testing is a constant time operation for OrderedSet, but a linear time operation for Array.

OrderedSet uses a standard array value for element storage, which can be extracted with minimal overhead. This is a great option if we want to pass the contents of an ordered set to a function that only takes an Array (or is generic over RangeReplaceableCollection or MutableCollection):

<span class="kd">func</span> <span class="nf">buildHouses</span><span class="p">(</span><span class="n">_</span> <span class="nv">houses</span><span class="p">:</span> <span class="kt">Array</span><span class="o"><</span><span class="kt">String</span><span class="o">></span><span class="p">)</span>

<span class="nf">buildHouses</span><span class="p">(</span><span class="n">buildingMaterials</span><span class="p">)</span> <span class="c1">// error</span>
<span class="nf">buildHouses</span><span class="p">(</span><span class="n">buildingMaterials</span><span class="o">.</span><span class="n">elements</span><span class="p">)</span> <span class="c1">// OK</span>

And for cases where SetAlgebra conformance is desired, OrderedSet provides an efficient unordered view of its elements that conforms to SetAlgebra:

<span class="kd">func</span> <span class="n">blowHousesDown</span><span class="o"><</span><span class="kt">S</span><span class="p">:</span> <span class="kt">SetAlgebra</span><span class="o">></span><span class="p">(</span><span class="n">_</span> <span class="nv">houses</span><span class="p">:</span> <span class="kt">S</span><span class="p">)</span> <span class="p">{</span> <span class="o">...</span> <span class="p">}</span>

<span class="nf">blowHousesDown</span><span class="p">(</span><span class="n">buildingMaterials</span><span class="p">)</span> <span class="c1">// error: `OrderedSet<String>` does not conform to `SetAlgebra`</span>
<span class="nf">blowHousesDown</span><span class="p">(</span><span class="n">buildingMaterials</span><span class="o">.</span><span class="n">unordered</span><span class="p">)</span> <span class="c1">// OK</span>

OrderedSet also implements some of the functionality of RangeReplaceableCollection and MutableCollection, and most of SetAlgebra. (Member uniqueness and order-sensitive equality prevent complete conformance.)

This is accomplished by maintaining an array of members (for efficient random-access traversal) and a hash table of indices into that array (for efficient membership testing). Because the indices stored inside the hash table can often be encoded into fewer bits than a standard Int, OrderedSet will often use less memory than a plain old Set!

OrderedDictionary

OrderedDictionary is a useful alternative to Dictionary when the order of elements is important or we need to be able to efficiently access elements at various positions within the collection.

We can create an ordered dictionary with any key type that conforms to the Hashable protocol:

<span class="k">let</span> <span class="nv">responses</span><span class="p">:</span> <span class="kt">OrderedDictionary</span> <span class="o">=</span> <span class="p">[</span>
  <span class="mi">200</span><span class="p">:</span> <span class="s">"OK"</span><span class="p">,</span>
  <span class="mi">403</span><span class="p">:</span> <span class="s">"Forbidden"</span><span class="p">,</span>
  <span class="mi">404</span><span class="p">:</span> <span class="s">"Not Found"</span><span class="p">,</span>
<span class="p">]</span>

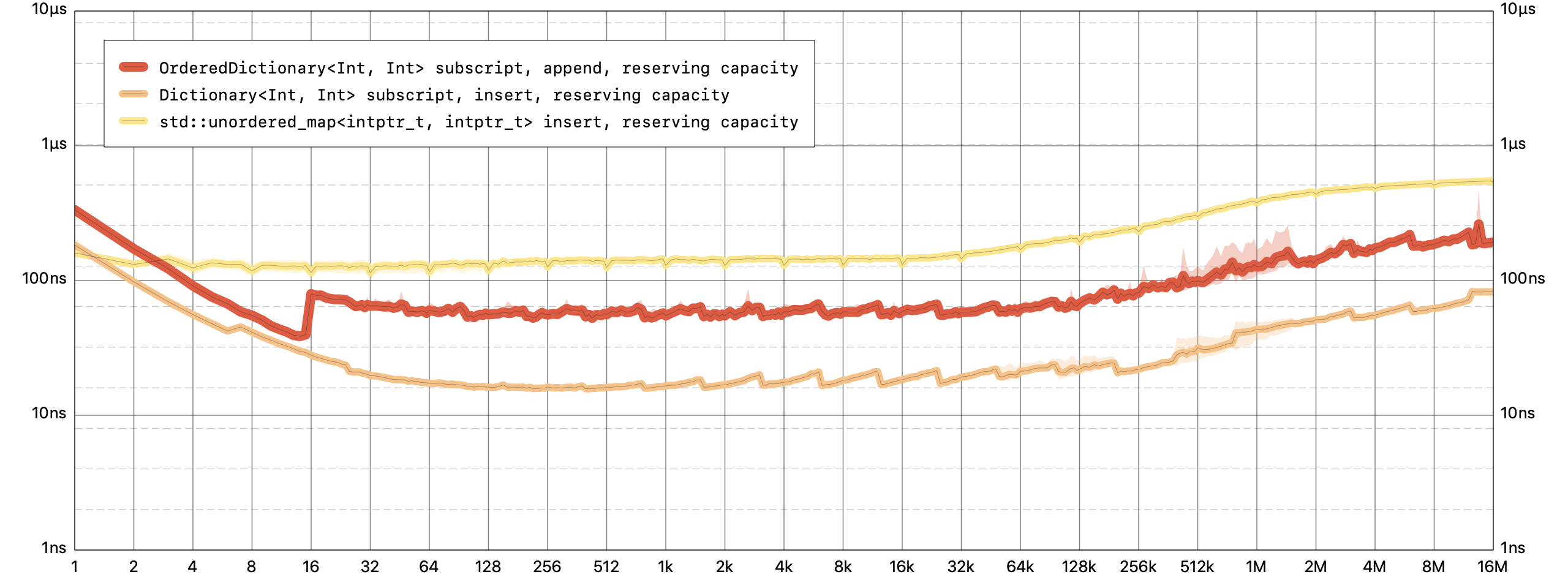
Inserting a new key-value pair into an OrderedDictionary appends it in constant time.

OrderedDictionary provides many of the same operations as Dictionary. For example, we can efficiently look up and add values using the familiar key-based subscript:

<span class="n">responses</span><span class="p">[</span><span class="mi">200</span><span class="p">]</span> <span class="c1">// "OK"</span>
<span class="n">responses</span><span class="p">[</span><span class="mi">500</span><span class="p">]</span> <span class="o">=</span> <span class="s">"Internal Server Error"</span>

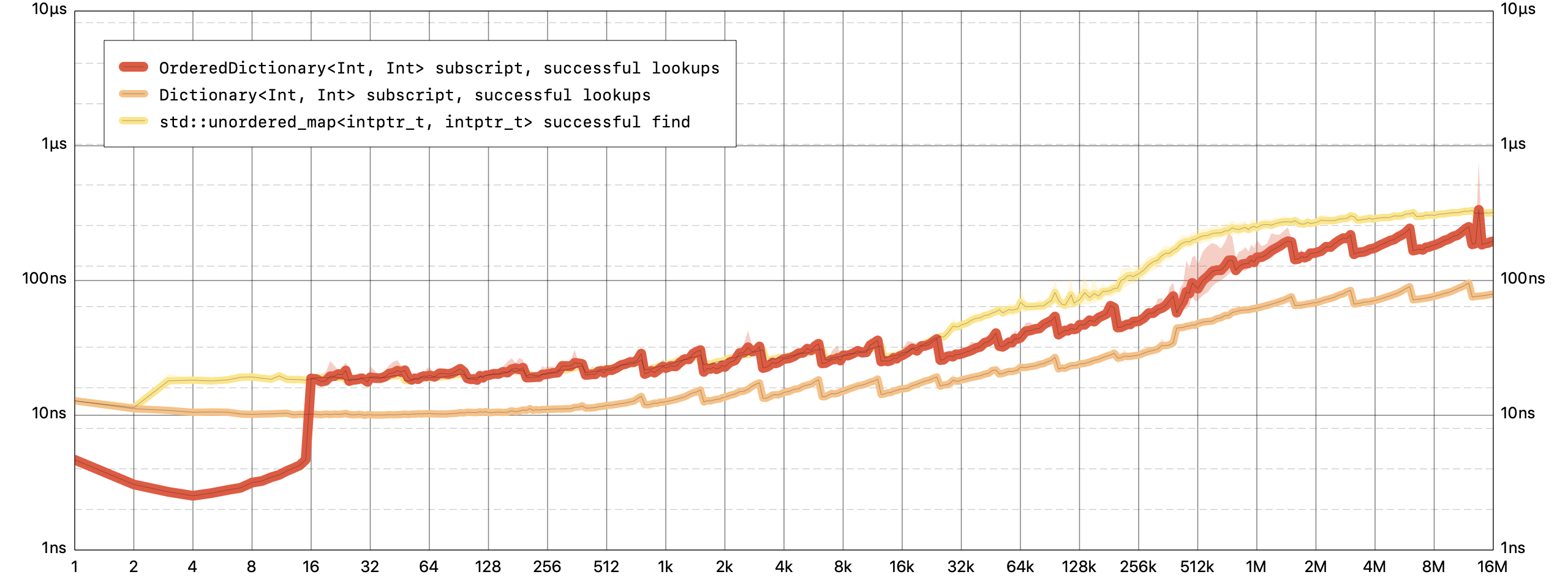
Looking up a value for a key is a constant time operation for OrderedDictionary.

If a new entry is added using the subscript setter, it gets appended to the end of the dictionary. So that by default, the dictionary contains its elements in the order they were originally inserted:

<span class="k">for</span> <span class="p">(</span><span class="n">code</span><span class="p">,</span> <span class="n">phrase</span><span class="p">)</span> <span class="k">in</span> <span class="n">responses</span> <span class="p">{</span>
  <span class="nf">print</span><span class="p">(</span><span class="s">"</span><span class="se">\(</span><span class="n">code</span><span class="se">)</span><span class="s"> (</span><span class="se">\(</span><span class="n">phrase</span><span class="se">)</span><span class="s">)"</span><span class="p">)</span>
<span class="p">}</span>
<span class="c1">// 200 (OK)</span>
<span class="c1">// 403 (Forbidden)</span>
<span class="c1">// 404 (Not Found)</span>
<span class="c1">// 500 (Internal Server Error)</span>

OrderedDictionary uses integer indices with the first element always beginning at 0. To avoid ambiguity between key-based and index-based subscripts, OrderedDictionary doesn’t conform to Collection directly. Instead it provides a random-access view over its key-value pairs:

<span class="n">responses</span><span class="p">[</span><span class="mi">0</span><span class="p">]</span> <span class="c1">// nil (key-based subscript)</span>
<span class="n">responses</span><span class="o">.</span><span class="n">elements</span><span class="p">[</span><span class="mi">0</span><span class="p">]</span> <span class="c1">// (200, "OK") (index-based subscript)</span>

Like the standard Dictionary, OrderedDictionary also provides lightweight keys and values views. The same index is portable across all of the views a dictionary vends into its contents:

<span class="k">if</span> <span class="k">let</span> <span class="nv">i</span> <span class="o">=</span> <span class="n">responses</span><span class="o">.</span><span class="nf">index</span><span class="p">(</span><span class="nv">forKey</span><span class="p">:</span> <span class="mi">404</span><span class="p">)</span> <span class="p">{</span>
  <span class="n">responses</span><span class="o">.</span><span class="n">keys</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="c1">// 404</span>
  <span class="n">responses</span><span class="o">.</span><span class="n">values</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="c1">// "Not Found"</span>
  <span class="n">responses</span><span class="o">.</span><span class="nf">remove</span><span class="p">(</span><span class="nv">at</span><span class="p">:</span> <span class="n">i</span> <span class="o">+</span> <span class="mi">1</span><span class="p">)</span> <span class="c1">// (500, "Internal Server Error")</span>
<span class="p">}</span>
<span class="c1">// `responses` is now [200: "OK", 403: "Forbidden", 404: "Not Found"]</span>

OrderedDictionary implements some of the functionality of MutableCollection and RangeReplaceableCollection, though its requirement for member uniqueness prevents it from implementing complete conformance for either protocol.

An ordered dictionary consists of an OrderedSet of keys, alongside a regular Array that contains their associated values. Each of these can be extracted with minimal overhead, which is an efficient option for interoperating with a function that expects a certain type.

Relation to the Swift Standard Library

It’s our ambition for the standard library to include a rich, pragmatic set of general-purpose data structures.

Similar to packages like Swift Numerics and Swift Algorithms, an important goal of the Collections package is to serve as a (relatively) low-friction proving ground for new data structure implementations, before they become ready to be proposed as official library additions through the regular Swift Evolution process.

The experience we gain using these constructs in package form will inform the eventual review discussion. It will also provide us an opportunity to correct any design issues before they get etched into stone.

The Collections package is, in part, a recognition of the challenges involved in contributing new data structures to Swift. Because the standard library is ABI-stable, a lot of time must be spent thinking about which parts of a data structure are going to be @frozen and which aren’t, and which methods should be @inlinable and touch those frozen internals.

Accordingly, the Collections package is not just a set of data structures. It is also a watering hole for contributors who want to learn more about the dark art of ABI design and a sophisticated toolkit to help meet the high standards of correctness and efficiency demanded of data structures.

However, just because an addition might be a good candidate for inclusion in the Collections package, it doesn’t need to begin its life there. This is not a change to the Swift Evolution process. Though the bar is high for new data structures, well-supported pitches will continue to be considered, as always.

Contribution Criteria

The immediate focus of this package is to incubate a pragmatic set of production grade data structures – similar to those you might find in the C++ containers library or the Java collections framework.

To be a good candidate for inclusion in the Collections package, a data structure should appreciably improve the performance or correctness of real-world Swift code, and its implementation strategy should take into account modern computer architecture and Swift’s performance characteristics.

The Collections package is not intended to be a comprehensive taxonomy of data structures. There are many classic data structures that don’t warrant inclusion, because they provide insufficient value over the existing types in the standard library or because alternatives with superior implementation strategies exist. (For example, it is unlikely we’d want to implement linked lists or red-black trees – the same niche can likely be better filled with high-fanout search trees such as in-memory B-trees.)

As the focus of this package is on providing production grade data structure implementations, the bar for inclusion is high. Some baseline criteria for evaluating contributions:

• Reliability. The implementation must work correctly without any unhandled edge cases, and it must continue working in the face of future language, compiler and standard library changes.To help with this work, the package includes support for writing combinatorial regression tests, as well as a library of semi-automated conformance checks for semantic protocol requirements.
• Runtime performance. The implementation must exhibit best-of-class performance on all practical working sets, from a single element to tens of millions. This doesn’t just mean asymptotic performance – constant factors matter, too!The package comes with an elaborate benchmarking module that can be used to exercise operations over all possible working set sizes. It’s what we used to create the benchmarks included in this blog post! We can use it to identify areas that need optimization work, and to evaluate potential optimizations based on hard data.
• Memory overhead. Memory is a scarce resource; the data structures we implement ought not spend too much of it on storing internal pointers, padding bytes, unused capacity or similar fluff. Once we decide on an implementation strategy, we should employ every trick in the book to minimize memory usage!

The best way to start work on a new data structure is to discuss it on the on the forum. This way we can figure out if the data structure would be right for the package, discuss implementation strategies, and plan to allocate capacity to help.

Get Involved!

Your experience, feedback, and contributions are very welcome!

• Get started by trying out the Swift Collections library on GitHub,
• Discuss the library, suggest improvements and get help in the Swift Collections forum,
• Open an issue with problems you find,
• or contribute a pull request to fix them!

Questions?

Please feel free to ask questions about this post in the associated thread on the Swift forums.

By Karoy Lorentey is an engineer on the Swift Standard Library team at Apple
Source Swift