Learn how to create and use custom easing functions in Compose

Everything that moves, accelerates, or decelerates — nothing starts or stops moving instantaneously. The ball you bounce on a floor hits the ground and then bounces back up again and eventually comes to a resting position after a few smaller bounces. A train door closes slowly as it reaches its destination. An easing function defines this acceleration or deceleration. Once you learn about easing functions you’ll start to notice easing functions all around you, and sometimes you won’t be able to see the world normally again (okay, maybe that’s just me).

When considering UI animations, using different easing functions can help communicate different types of animations. For example, if you want a more playful UI — you may consider using an easing function that bounces or overshoots. For a more fluid animation, you may consider using an ease in or ease out function.

What is an easing function?

Analogous to Interpolators from the View system, an Easing function in Compose is a way to describe the rate of change, let’s say y over time (which is usually represented on a graph as x) . The function maps the input (fraction of the animation duration) from 0 to 1.

The interface for implementing easing functions in Compose is as follows:

It passes in a fraction — between 0 and 1, and maps it to a new value as the result of applying the transformation. So the simplest example is to implement a Linear easing function:

In the example below the input fraction represents progress over time (time being the x axis). The linear mapping would return that same progress value, therefore the rate of change is constant over time:

However, rarely does a linear easing function look the best for animations — as most things in life don’t move linearly, gravity almost always affects how objects move. Sure, linear easing is way better than not having any animation at all, but it doesn’t look nearly as fluid as curves that ease over time.

Implementing your own Easing Function

If you’ve looked into the source for Compose’s Easing functions, you may have noticed that there are a few defined easing functions for you to use, but you are also able to implement your own easing function if you’d like something more custom. You may have seen some of the standard easing functions provided are using CubicBezierEasing function and providing it some values:

This looks simple enough! But what is CubicBezierEasing? Before we get into that, let’s learn a bit of theory about Bézier curves in general.

What is a Bézier curve? 🤔

A Bézier curve is a parametric curve controlled by a set of control points. These control points determine the shape of the curve. You’ve probably seen a Bézier curve without realizing it — if you’ve tried to draw vector art by creating points and lines are created between them — this is a usage of Bézier curves. They offer a way to get smooth transitions between points — through a mathematical formula.

How do Bézier curves work?

We can start a Bézier curve with two points — p0 and p1, connected by a line. If we introduce a third point P between these two points, the position of P is described by what is called a t value — a value between 0 and 1 (or a fraction).

As t moves between 0 and 1, P moves along the line formed by p0 and p1, P’s value is a combination of the two points. For example: as t moves closer to p1, it moves towards 1, and as t moves closer to p0 it moves closer to 0, and any values in between are a mix of the two values. This is called lerp or linear interpolation.

P = (1-t)p0 + t * p1

Adding another point to our sample, we have p0, p1, and p2. We now have two interpolated points, moving on their lines based on the same t value. After connecting these two points with another line, and if we add another point on that line that also moves based on the same t-value. This follows a very specific path which is known as a quadratic Bézier curve path. You can keep adding points to get more complicated curves, but the same formula will still apply.

For a more detailed visual description on Bézier curves, this video on The Beauty of Bézier Curves is worth watching, and reading this Primer on Bézier Curves book.

What is a cubic Bézier curve?

A cubic Bézier curve follows the same pattern as above, but it takes in 4 (p0, p1, p2, p3) points to produce a curve (hence the cubic name). The shape of the curve is determined by the control points p1 and p2.

The CubicBezierEasing function takes in two of the control points p1 and p2. p1’s x and y are the first two parameters of the function, and p2’s x and y are the second two parameters of the function. p0 and p3 are static at (0,0) and (1, 1) — so they are not taken as input into the function.

Implementing a Custom Easing Function

To define our own custom easing function, we can implement the Easing function interface ourselves — or use the existing CubicBezierEasing function that is already defined. Luckily, we don’t need to figure out beautiful looking easing curves ourselves! Looking at the easings.net set of functions, we can take the cubic bezier points from the site and implement most of the easing functions.

For example the EaseInOut function can be easily defined in the following way:

The points mapped that make up the easing curve look as follows:

In the above diagram, you’ll see the points p1 with the x,y value of (0.42, 0.0f) and p2 with the x,y value of (0.58f, 1.0f). This will produce the following kind of easing curve. As you can see the animation starts off slowly, evens out to linear and then slows down towards the end:

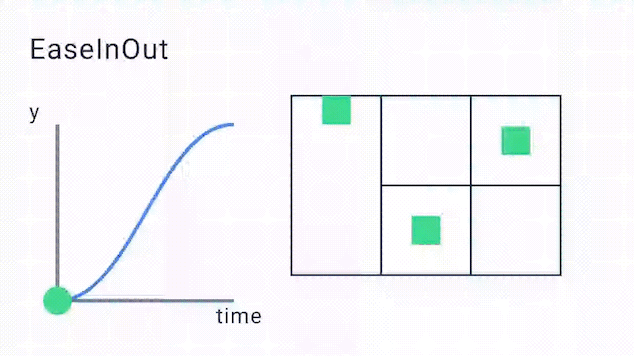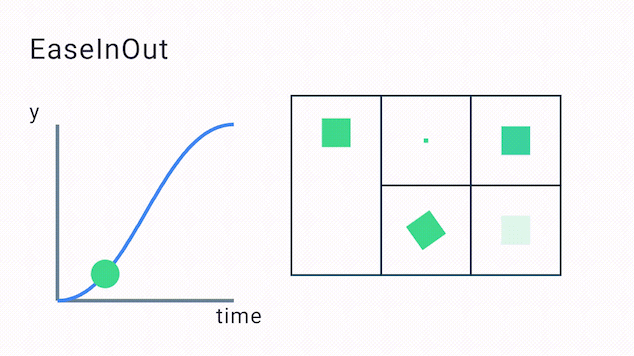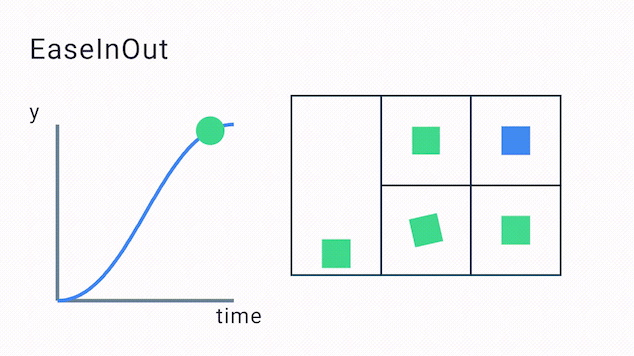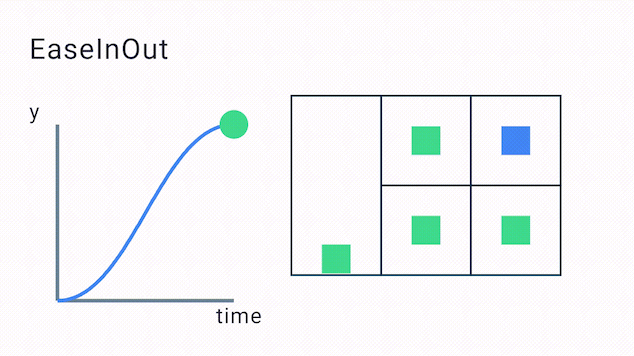
Some easing functions don’t need to use cubic Bézier curves and instead transform the value using specified formulas, like the ease out bounce function.

This is an example of implementing the EaseOutBounce easing function (taken from easings.net):

This will produce the following easing curve:

We can also build our own custom easing curve using cubic-bezier.com — tweaking it to our heart’s desire.

How can I use a Custom Easing Function with my Compose Animations?

Almost all the animation APIs accept an animationSpec parameter. We can specify the easing curve to use by using the tween() animationSpec and setting the easing parameter to your custom easing function:

There are a few more options for different animationSpecs — such as spring() animation, a physics-based animation. It is worth noting that spring() is the default AnimationSpec as it can handle interruptions more smoothly than duration-based AnimationSpec types such as tween. Spring guarantees the continuity of velocity when target value changes amid animations. Another animationSpec option is keyframes() for more fine-grain control at different times in your animation. Read more about different animationSpecs in the AnimationSpec documentation.

Show me the difference!

Consider the Crane calendar selection animation, we can set the easing curve of the whole animation to an EaseOutQuart:

Here is a side-by-side comparison of the animation with different easing curves, you can see that using the Linear vs. custom-defined EaseOutQuart easing function produces two very different looking animations. The ease out animation is smoother and feels more fluid, whereas the linear one feels very structured and is not very natural looking.

Linear Easing — same consistent speed throughout the whole animation, the ending is abrupt, vs EaseOutQuart — slows down towards the end, a much smoother ending:

Summary

If you’d like to use other easing functions, 1.2.0-beta03 of Compose Animation introduces a bunch of new Easing functions for you to use. Check out the Easing documentation here for the updated list of new easing functions.

That’s all for now — I hope you’ll be looking at everyday objects to try to figure out what easing function they are using.

If you have any questions, feel free to reach out to me on Twitter @riggaroo.

Bye for now! 👋

Thanks to Doris Liu, Nick Butcher and Ben Trengrove for the feedback and reviews on this post.